
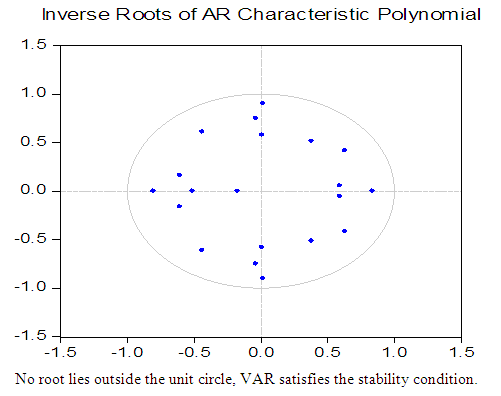
Robustness of the estimates depends on the extent, or persistence, of the autocorrelations affecting current observations. More conservative significance levels for the t-tests are advised. The result is that interval estimation and hypothesis testing become unreliable. Because autocorrelations in economic data are likely to be positive, reflecting similar random factors and omitted variables carried over from one time period to the next, variance estimates tend to be biased downward, toward t-tests with overly optimistic claims of accuracy. Compounding the problem, autocorrelation introduces bias into the standard variance estimates, even asymptotically. This is a significant problem in small samples, where confidence intervals will be relatively large. In the presence of autocorrelation, OLS estimates remain unbiased, but they no longer have minimum variance among unbiased estimators. A small amount of heteroscedasticity is also apparent, though it is difficult for a visual assessment to separate this from random variation in such a small sample. There appears to be some evidence of autocorrelation in several of the persistently positive or negative departures from the mean, particularly in the undifferenced data.
Residual graph series#
The scale of the residuals is several orders of magnitude less than the scale of the original data (see the example Time Series Regression I: Linear Models), which is a sign that the models have captured a significant portion of the data-generating process (DGP). For each model, the residuals scatter around a mean near zero, as they should, with no obvious trends or patterns indicating misspecification.


 0 kommentar(er)
0 kommentar(er)
